Where is Thailand located on the world map?
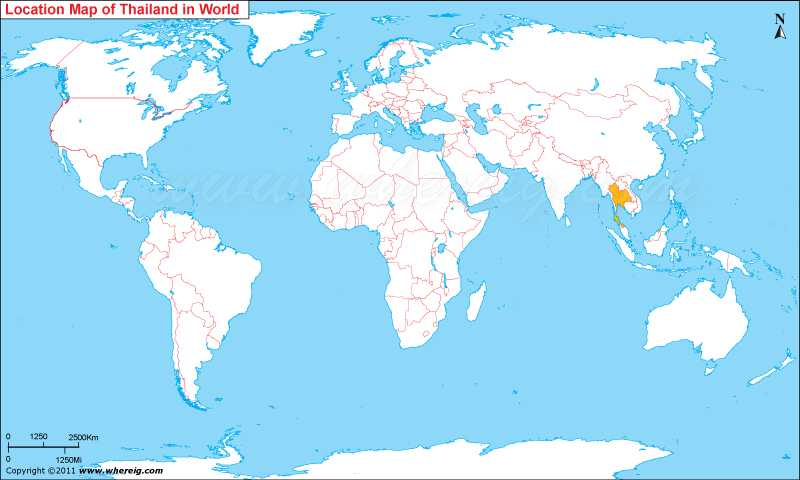
The given Thailand location map shows that Thailand is located in the South-east Asia. Thailand map also shows that it shares its international boundaries with Laos in the east, Cambodia in the south-east, Malaysia in the south, and Myanmar (Burma) in the west. Besides, in the south, it has coastline along the Gulf of Thailand and in the south-west Andaman Sea. The climate type of Thailand is tropical with monsoons characteristics.
Bangkok is the capital city of Thailand; it is also the largest and focal point of commercial, industrial, and cultural activities. The government type of Thailand is currently a constitutional monarchy; wherein a hereditary monarch is head of state and the Prime Minister is the head of government. However, the judiciary is independent of the executive and the legislative branches.
The economy of the country is greatly flourishing with the growth of services, industrialization along with agriculture produce. Major goods that Thailand exports are Thai rice, textiles, rubber, footwear, fishery products, jewellery, computers, cars, and electrical appliances. Among these exports, Thailand rice is world famous and hence Thailand is the world's no.1 exporter of rice. In addition, Thailand tourism is also growing especially tourism Prostitution in Thailand and sex tourism in Thailand has some percentage in total GDP of the country. Above all, sex tourism in Thailand is a de facto part of the economy.
Where is Thailand Located?
The given Thailand location map shows that Thailand is located in the South-east Asia. Thailand map also shows that it shares its international boundaries with Laos in the east, Cambodia in the south-east, Malaysia in the south, and Myanmar (Burma) in the west. Besides, in the south, it has coastline along the Gulf of Thailand and in the south-west Andaman Sea. The climate type of Thailand is tropical with monsoons characteristics.
Bangkok is the capital city of Thailand; it is also the largest and focal point of commercial, industrial, and cultural activities. The government type of Thailand is currently a constitutional monarchy; wherein a hereditary monarch is head of state and the Prime Minister is the head of government. However, the judiciary is independent of the executive and the legislative branches.
The economy of the country is greatly flourishing with the growth of services, industrialization along with agriculture produce. Major goods that Thailand exports are Thai rice, textiles, rubber, footwear, fishery products, jewellery, computers, cars, and electrical appliances. Among these exports, Thailand rice is world famous and hence Thailand is the world's no.1 exporter of rice. In addition, Thailand tourism is also growing especially tourism Prostitution in Thailand and sex tourism in Thailand has some percentage in total GDP of the country. Above all, sex tourism in Thailand is a de facto part of the economy.
Location Map of Asian Countries
- Where is Afghanistan
- Where is Armenia
- Where is Azerbaijan
- Where is Bahrain
- Where is Bangladesh
- Where is Bhutan
- Where is Brunei
- Where is Cambodia
- Where is China
- Where is Georgia
- Where is Hong Kong
- Where is India
- Where is Indonesia
- Where is Iran
- Where is Iraq
- Where is Israel
Popular Asian Cities
- Where is Abu Dhabi
- Where is Amman
- Where is Ankara
- Where is Baghdad
- Where is Baku
- Where is Bangkok
- Where is Bangalore
- Where is Beijing
- Where is Bishkek
- Where is Damascus
- Where is Dhaka
- Where is Dubai